Преобразование графиков функций

В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции получить график функции

Линейным преобразованием функции называется преобразование самой функции и/или ее аргумента к виду , а также преобразование, содержащее модуль аргумента и/или функции.

Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:

1. Вычленение базовой функции, собственно, график которой мы и преобразовываем.
2. Определения порядка преобразований.

И менно на этих моментах мы и остановимся подробнее.

Рассмотрим внимательно функцию

В ее основе лежит функция . Назовем ее базовой функцией .

При построении графика функции мы совершаем преобразования графика базовой функции .

Если бы мы совершали преобразования функции в том же порядке, в каком находили ее значение при определенном значении аргумента, то

Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.

Преобразования аргумента.

1. f(x) f(x+b)

1. Строим график фунции

2. Сдвигаем график фунции вдоль оси ОХ на |b| единиц

• влево, если b>0
• вправо, если b<0

Построим график функции

1. Строим график функции

2. Сдвигаем его на 2 единицы вправо:

2. f(x) f(kx)

1. Строим график фунции

2. Абсциссы точек графика делим на к, ординаты точек оставляем без изменений.

Построим график функции .

1. Строим график функции

2. Все абсциссы точек графика делим на 2, ординаты оставляем без изменений:

3. f(x) f(-x)

1. Строим график фунции

2. Отображаем его симметрично относительно оси OY.

Построим график функции .

1. Строим график функции

2. Отображаем его симметрично относительно оси OY:

4. f(x) f(|x|)

1. Строим график функции

2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:

График функции выглядит так:

Построим график функции

1. Строим график функции (это график функции , смещенный вдоль оси ОХ на 2 единицы влево):

2. Часть графика, расположенную левее оси OY (x<0) стираем:

3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:

Важно! Два главных правила преобразования аргумента.

1. Все преобразования аргумента совершаются вдоль оси ОХ

2. Все преобразования аргумента совершаются "наоборот" и "в обратном порядке".

Например, в функции последовательность преобразований аргумента такая:

1. Берем модуль от х.

2. К модулю х прибавляем число 2.

Но построение графика мы совершали в обратном порядке:

Сначала выполнили преобразование 2. - сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы "наоборот")

Затем выполнили преобразование f(x) f(|x|).

Коротко последовательность преобразований записывается так:

Теперь поговорим о преобразовании функции . Преобразования совершаются

1. Вдоль оси OY.

2. В той же последовательности, в какой выполняются действия.

Вот эти преобразования:

1. f(x)f(x)+D

2. Смещаем его вдоль оси OY на |D| единиц

• вверх, если D>0
• вниз, если D<0

Построим график функции

1. Строим график функции

2. Смещаем его вдоль оси OY на 2 единицы вверх:

2. f(x)Af(x)

1. Строим график функции y=f(x)

2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.

Построим график функции

1. Построим график функции

2. Ординаты всех точек графика умножим на 2:

3. f(x)-f(x)

1. Строим график функции y=f(x)

Построим график функции .

1. Строим график функции .

2. Отображаем его симметрично относительно оси ОХ.

4. f(x)|f(x)|

1. Строим график функции y=f(x)

2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.

Построим график функции

1. Строим график функции . Он получается смещением графика функции вдоль оси OY на 2 единицы вниз:

2. Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:

И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:

|y|=f(x)

1. Строим график функции y=f(x)

2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.

Построим график уравнения

1. Строим график функции :

2. Часть графика, расположенную ниже оси ОХ стираем:

3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.

И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции

График этой функции выглядит так:

Какие из данных функций имеют обратную? Для таких функций найти обратные функции:

4.12. а)	y = x ;					б) y = 6 −3 x ;
г) y =						д) y = 2 x 3 +5 ;
4.13. а)	y = 4 x − 5 ;						y = 9 − 2 x − x 2 ;
	y = sign x ;						y =1 + lg(x + 2) ;

	y = 2 x 2 +1 ;
			x − 2
						при x < 0
в) y =		−x
						при x ≥ 0

Выяснить, какие из данных функций монотонны, какие – строго монотонны, а какие – ограничены:

4.14. а)

f (x) = c, c R ;

б) f (x ) = cos 2 x ;

в) f (x ) = arctg x ;

г) f (x ) = e 2 x ;

д) f (x ) = −x 2 + 2 x ;

е) f (x ) =

2x + 5

y = ctg7 x .

4.15. а)

f (x ) = 3− x

б) f (x ) =

f (x) =

x + 3

x + 6

x < 0,

3x + 5

г) f (x ) = 3 x 3 − x ;

− 10 при

f (x) =

д) f (x ) =

x 2 при

x ≥ 0;

x + 1

f (x ) = tg(sin x ).

4.2. Элементарные функции. Преобразование графиков функций

Напомним, что графиком функции f (x ) в декартовой прямоугольной системе координат Oxy называется множество всех точек плоскости с координатами (x , f (x )) .

Часто график функции y = f (x ) можно построить с помощью преобразований (сдвиг, растяжение) графика некоторой уже известной функции.

В частности, из графика функции y = f (x ) получается график функции:

1) y = f (x ) + a – сдвигом вдоль оси Oy на a единиц (вверх, если a > 0 , и вниз, если a < 0 ;

2) y = f (x −b ) – сдвигом вдоль оси Ox на b единиц (вправо, если b > 0 ,

и влево, если b < 0 ;

3) y = kf (x ) – растяжением вдоль оси Oy в k раз;

4) y = f (mx ) – сжатием по оси Ox в m раз;

5) y = − f (x ) – симметричным отражением относительно оси Ox ;

6) y = f (−x ) – симметричным отражением относительно оси Oy ;

7) y = f (x ) , следующим образом: часть графика, расположенная не

ниже оси Ox , остается без изменений, а «нижняя» часть графика симметрично отражается относительно оси Ox ;

8) y = f (x ) , следующим образом: правая часть графика (при x ≥ 0 )

остается без изменений, а вместо «левой» строится симметричное отражение «правой» относительно оси Oy .

Основными элементарными функциями называются:

1) постоянная функция y = c ;

2) степенная функция y = x α , α R ;

3) показательная функция y = a x , a ≠ 0, a ≠1 ;

4) логарифмическая функция y = log a x , a > 0, a ≠ 1 ;

5) тригонометрические функции y = sin x , y = cos x , y = tg x ,

y = ctg x , y = sec x (где sec x = cos 1 x ), y = cosec x (где cosec x = sin 1 x );

6) обратные тригонометрические функции y = arcsin x , y = arccos x , y = arctg x , y = arcctg x .

Элементарными функциями называются функции, полученные из основных элементарных функций с помощью конечного числа арифметических операций (+, − , ÷) и композиций (т.е. образования сложных функций f g ).

Пример 4.6. Построить график функции

1) y = x 2 + 6 x + 7 ; 2) y = −2sin 4 x .

Решение: 1) путем выделения полного квадрата функция преобразуется к виду y = (x +3) 2 − 2 , поэтому график данной функции можно получить из графика функции y = x 2 . Достаточно сначала сместить параболу y = x 2 на три единицы влево (получим график функции y = (x +3) 2 ), а затем на две единицы вниз (рис. 4.1);

	стандартную	синусоиду						y = sin x	в четыре раза по оси		Ox ,
получим график функции y = sin 4 x (рис. 4.2).
										y= sin4x
										y=sin x

Растянув полученный график в два раза вдоль оси Oy , получим график функции y = 2sin 4 x (рис. 4.3). Осталось отразить последний график относительно оси Ox . Результатом будет искомый график(см. рис. 4.3).

						y= 2sin4x

y=– 2sin4 x

Задачи для самостоятельного решения

Построить графики следующих функции, исходя из графиков основных элементарных функций:

4.16. а) y = x 2 −6 x +11 ;

4.17. а) y = −2sin(x −π ) ;

4.18. а) y = − 4 x −1 ;

4.19. а) y = log 2 (−x ) ;

4.20. a) y = x +5 ;

4.21. а) y = tg x ;

4.22. а) y = sign x ;

4.23. а) y = x x + + 4 2 ;

y = 3 − 2 x − x 2 .

y = 2cos 2 x .

В зависимости от условий протекания физических процессов одни величины принимают постоянные значения и называются константами, другие - изменяются в определенных условиях и называются переменными.

Внимательное изучение окружающей среды показывает, что физические величины зависимы друг от друга, т. е. изменение одних величин влечет за собой изменение других.

Математический анализ занимается изучением количественных соотношений взаимно -изменяющихся величин, отвлекаясь от конкретного физического смысла. Одним из основных понятий математического анализа есть понятие функции.

Рассмотрим элементы множества и элементы множества
(рис. 3.1).

Если устанавливается некоторое соответствие между элементами множеств
и в виде правила , то тем самым отмечают, что определяется функция
.

Определение 3.1. Соответствие, которое связывает с каждым элементомне пустого множества
некоторый, вполне определенный, элементне пустого множества ,называется функцией или отображением
в .

Символически отображение
в записывается следующим образом:

.

При этом множество
называется областью определения функции и обозначается
.

В свою очередь, множество называется областью значений функции и обозначается
.

Кроме того, необходимо отметить, что элементы множества
называют независимыми переменными, элементы множества называют зависимыми переменными.

Способы задания функции

Функция может задаваться следующими основными способами: табличным, графическим, аналитическим.

Если на основании экспериментальных данных составляют таблицы, в которых содержатся значения функции и соответствующие им значения аргумента, то такой способ задания функции называют табличным.

В то же время, если некоторые исследования результата эксперимента выводят на регистратор (осциллограф, самописец и т. д.), то отмечают, что функция задается графически.

Наиболее распространенным есть аналитический способ задания функции, т.е. способ, при котором с помощью формулы связывают независимую и зависимую переменные. При этом существенную роль играет область определения функции:

разные, хотя они и задаются одинаковыми аналитическими соотношениями.

Если задают только формулу функции
, то считают, что область определения этой функции совпадает с множеством тех значений переменной, для которых выражение
имеет смысл. В этой связи особую роль играет проблема нахождения области определения функции.

Задача 3.1. Найти область определения функции

Решение

Первое слагаемое принимает действительные значения при
,а второе при. Таким образом, для нахождения области определения заданной функции необходимо решить систему неравенств:

В результате решения такой системы получают . Следовательно, область определения функции есть отрезок
.

Простейшие преобразования графиков функций

Построение графиков функций можно существенно упростить, если пользоваться известными графиками основных элементарных функций. Основными элементарными функциями называются следующие функции:

1)степенная функция
где
;

2)показательная функция
где
и
;

3)логарифмическая функция
, где -любое положительное число, отличное от единицы:
и
;

4)тригонометрические функции




;
.

5)обратные тригонометрические функции
;
;
;
.

Элементарными функциями называются функции, получающиеся из основных элементарных функций с помощью четырех арифметических действий и суперпозиций, примененных конечное число раз.

Простые геометрические преобразования также позволяют упростить процесс построения графика функций. Эти преобразования основываются на следующих утверждениях:

График функции y=f(x+a) есть графикy=f(x), сдвинутый (при a >0 влево, при a < 0 вправо) на |a| единиц параллельно осиOx.

График функции y=f(x) +bесть графикy=f(x), сдвинутый (приb>0 вверх, приb< 0 вниз) на |b| единиц параллельно осиOy.

График функции y = mf(x) (m0) есть график y = f(x), растянутый (приm>1) вmраз или сжатый (при 0

График функции y = f(kx) есть график y = f(x), сжатый (при k >1) в k раз или растянутый (при 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.

Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.

Рассмотрим на примере квадратичной функции вида y = - 1 3 x + 2 3 2 + 2 , графиком которой является парабола y = x 2 , которая сжата втрое относительно О у и симметрична относительно О х, причем сдвинутую на 2 3 по О х вправо, на 2 единицы по О у вверх. На координатной прямой это выглядит так:

Yandex.RTB R-A-339285-1

Геометрические преобразования графика функции

Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ± k 1 · f (± k 2 · (x + a)) + b , когда k 1 > 0 , k 2 > 0 являются коэффициентами сжатия при 0 < k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 > 1 , k 2 > 1 вдоль О у и О х. Знак перед коэффициентами k 1 и k 2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по О х и по О у.

Определение 1

Существует 3 вида геометрических преобразований графика :

• Масштабирование вдоль О х и О у. На это влияют коэффициенты k 1 и k 2 при условии не равности 1 , когда 0 < k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 > 1 , k 2 > 1 , то график растягивается по О у и сжимается по О х.
• Симметричное отображение относительно координатных осей. При наличии знака « - » перед k 1 симметрия идет относительно О х, перед k 2 идет относительно О у. Если « - » отсутствует, тогда пункт при решении пропускается;
• Параллельный перенос (сдвиг) вдоль О х и О у. Преобразование производится при наличии коэффициентов a и b неравных 0 . Если значение a положительное, до график сдвигается влево на | а | единиц, если отрицательное a , тогда в право на такое же расстояние. Значение b определяет движение по оси О у, что значит при положительном b функция движется вверх, при отрицательном – вниз.

Рассмотрим решения на примерах, начиная со степенной функции.

Пример 1

Преобразовать y = x 2 3 и построить график функции y = - 1 2 · 8 x - 4 2 3 + 3 .

Решение

Представим функции таким образом:

y = - 1 2 · 8 x - 4 2 3 + 3 = - 1 2 · 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Где k 1 = 2 , стоит обратить внимание на наличие « - » , а = - 1 2 , b = 3 . Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль О у вдвое, отображается симметрично относительно О х, сдвигается вправо на 1 2 и вверх на 3 единицы.

Если изобразить исходную степенную функцию, получим, что

при растягивании вдвое вдоль О у имеем, что

Отображение, симметричное относительно О х, имеет вид

а движение вправо на 1 2

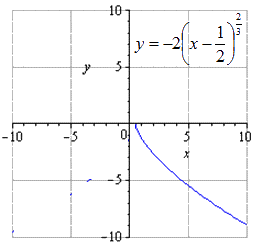
движение на 3 единицы вверх имеет вид

Преобразования показательной функции рассмотрим на примерах.

Пример 2

Произвести построение графика показательной функции y = - 1 2 1 2 (2 - x) + 8 .

Решение.

Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 · 1 2 - 1 2 x + 8

Отсюда видно, что получим цепочку преобразований y = 1 2 x:

y = 1 2 x → y = 1 2 · 1 2 x → y = 1 2 · 1 2 1 2 x → → y = - 1 2 · 1 2 1 2 x → y = - 1 2 · 1 2 - 1 2 x → → y = - 1 2 · 1 2 - 1 2 x + 8

Получаем, что исходная показательная функция имеет вид

Сжимание вдвое вдоль О у дает

Растягивание вдоль О х

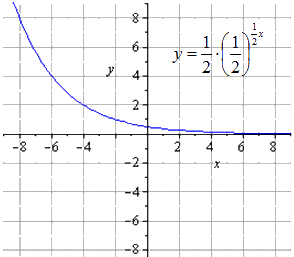
Симметричное отображение относительно О х

Отображение симметрично относительно О у

Сдвигание на 8 единиц вверх

Рассмотрим решение на примере логарифмической функции y = ln (x) .

Пример 3

Построить функцию y = ln e 2 · - 1 2 x 3 при помощи преобразования y = ln (x) .

Решение

Для решения необходимо использовать свойства логарифма, тогда получаем:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Преобразования логарифмической функции выглядят так:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Изобразим график исходной логарифмической функции

Производим сжимание строе по О у

Производим растягивание вдоль О х

Производим отображение относительно О у

Производим сдвигание вверх на 2 единицы, получаем

Для преобразования графиков тригонометрической функциинеобходимо подгонять под схему решения вида ± k 1 · f (± k 2 · (x + a)) + b . Необходимо, чтобы k 2 приравнивался к T k 2 . Отсюда получаем, что 0 < k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Рассмотрим примеры решения заданий с преобразованиями y = sin x .

Пример 4

Построить график y = - 3 sin 1 2 x - 3 2 - 2 с помощью преобразований функции y=sinx.

Решение

Необходимо привести функцию к виду ± k 1 · f ± k 2 · x + a + b . Для этого:

y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2

Видно, что k 1 = 3 , k 2 = 1 2 , a = - 3 , b = - 2 . Так как перед k 1 имеется « - » , а перед k 2 - нет, тогда получим цепочку преобразований вида:

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2

Подробное преобразование синусоиды. При построении графика исходной синусоиды y = sin (x) получаем, что наименьшим положительным периодом считается T = 2 π . Нахождение максимума в точках π 2 + 2 π · k ; 1 , а минимума - - π 2 + 2 π · k ; - 1 , k ∈ Z .

Производится растягивание по О у втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T = 2 π - это наименьший положительный период. Максимумы переходят в π 2 + 2 π · k ; 3 , k ∈ Z , минимумы - - π 2 + 2 π · k ; - 3 , k ∈ Z .

При растягивании по О х вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T = 2 π k 2 = 4 π . Максимумы переходят в π + 4 π · k ; 3 , k ∈ Z , минимумы – в - π + 4 π · k ; - 3 , k ∈ Z .

Изображение производится симметрично относительно О х. Наименьший положительный период в данном случае не меняется и равняется T = 2 π k 2 = 4 π . Переход максимума выглядит как - π + 4 π · k ; 3 , k ∈ Z , а минимума – π + 4 π · k ; - 3 , k ∈ Z .

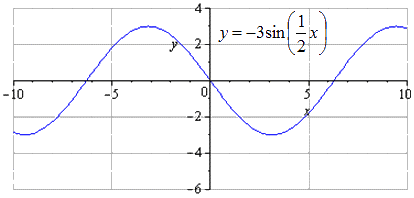
Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки - π + 3 + 4 π · k ; 1 , k ∈ Z , минимумов - π + 3 + 4 π · k ; - 5 , k ∈ Z .

На данном этапе график тригонометрической функции считается преобразованным.

Рассмотрим подробное преобразование функции y = cos x .

Пример 5

Построить график функции y = 3 2 cos 2 - 2 x + 1 при помощи преобразования функции вида y = cos x .

Решение

По алгоритму необходимо заданную функцию привести к виду ± k 1 · f ± k 2 · x + a + b . Тогда получаем, что

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Из условия видно, что k 1 = 3 2 , k 2 = 2 , a = - 1 , b = 1 , где k 2 имеет « - » , а перед k 1 он отсутствует.

Отсюда получаем, что получится график тригонометрической функции вида:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1)) → y = 3 2 cos - 2 (x - 1) + 1

Пошаговое преобразование косинусоиды с графической иллюстрацией.

При заданной графике y = cos (x) видно, что наименьший общий период равняется T = 2 π . Нахождение максимумов в 2 π · k ; 1 , k ∈ Z , а минимумов π + 2 π · k ; - 1 , k ∈ Z .

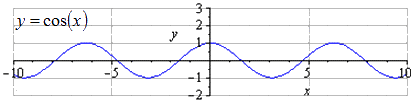
При растягивании вдоль О у в 3 2 раза происходит возрастание амплитуды колебаний в 3 2 раза. T = 2 π является наименьшим положительным периодом. Нахождение максимумов в 2 π · k ; 3 2 , k ∈ Z , минимумов в π + 2 π · k ; - 3 2 , k ∈ Z .

При сжатии вдоль О х вдвое получаем, что наименьшим положительным периодом является число T = 2 π k 2 = π . Производится переход максимумов в π · k ; 3 2 , k ∈ Z ,минимумов - π 2 + π · k ; - 3 2 , k ∈ Z .

Симметричное отображение относительно О у. Так как график нечетный, то он не будет изменяться.

При сдвигании графика на 1 . Отсутствуют изменения наименьшего положительного периода T = π . Нахождение максимумов в π · k + 1 ; 3 2 , k ∈ Z , минимумов - π 2 + 1 + π · k ; - 3 2 , k ∈ Z .

При сдвигании на 1 наименьший положительный период равняется T = π и не изменен. Нахождение максимумов в π · k + 1 ; 5 2 , k ∈ Z , минимумов в π 2 + 1 + π · k ; - 1 2 , k ∈ Z .

Преобразования функции косинуса завершено.

Рассмотрим преобразования на примере y = t g x .

Пример 6

Построить график функции y = - 1 2 t g π 3 - 2 3 x + π 3 при помощи преобразований функции y = t g (x) .

Решение

Для начала необходимо привести заданную функцию к виду ± k 1 · f ± k 2 · x + a + b , после чего получаем, что

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Отчетливо видно, что k 1 = 1 2 , k 2 = 2 3 , a = - π 2 , b = π 3 , а перед коэффициентами k 1 и k 2 имеется « - » . Значит, после преобразования тангенсоиды получаем

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Поэтапное преобразование тангенсоиды с графическим изображением.

Имеем, что исходный график – это y = t g (x) . Изменение положительного периода равняется T = π . Областью определения считается - π 2 + π · k ; π 2 + π · k , k ∈ Z .

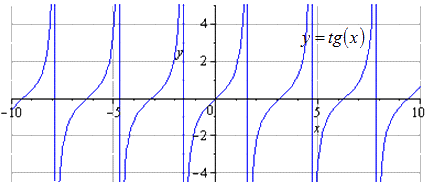
Сжимаем в 2 раза вдоль О у. T = π считается наименьшим положительным периодом, где область определения имеет вид - π 2 + π · k ; π 2 + π · k , k ∈ Z .

Растягиваем вдоль О х в 3 2 раза. Вычислим наименьший положительный период, причем равнялся T = π k 2 = 3 2 π . А область определения функции с координатами - 3 π 4 + 3 2 π · k ; 3 π 4 + 3 2 π · k , k ∈ Z , меняется только область определения.

Симметрия идет по сторону О х. Период не изменится в этот момент.

Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение О х и О у, тогда преобразуем до исходной функции.

Решение

Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций a r c sin x + a r c o cos x = π 2 . Значит, получим, что a r c sin x = π 2 - a r c cos x .

Видно, что y = a r c cos x → y = - a r c cos x → y = - a r c cos x + π 2 .

Поэтапное преобразование арккосинуса и графическое изображение.

График, данный по условию

Производим отображение относительно О х

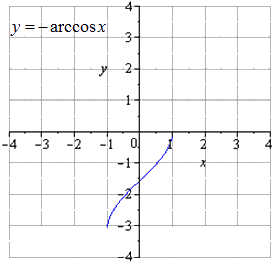
Производим движение вверх на π 2 .

Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.

Видно, что k 1 = 2 , k 2 = 1 3 , a = - 1 , b = 0 , где отсутствует знак « - » у k 1 и k 2 .

Отсюда получаем, что преобразования y = a r c sin x примет вид:

y = a r c sin (x) → y = 2 a r c sin (x) → → y = 2 a r c sin 1 3 x → y = 2 a r c sin 1 3 (x - 1)

Поэтапное преобразование графика арксинуса и графическое изображение.

График y = a r c sin x имеет область определения вида x ∈ - 1 ; 1 , тогда интервал y ∈ - π 2 ; π 2 относится к области значений.

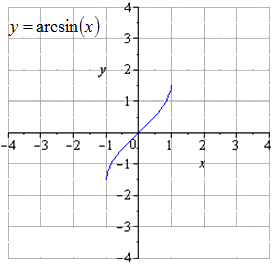
Необходимо растянуть вдвое по О у, причем область определения останется неизменной x ∈ - 1 ; 1 , а область значений y ∈ - π ; π .

Растягивание по О х строе. Происходит расширение области определения x ∈ - 3 ; 3 , но область значений остается неизменной y ∈ - π ; π .

, Конкурс «Презентация к уроку»

Презентация к уроку

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока: Определить закономерности преобразования графиков функций.

Задачи:

Образовательная:

• Научить обучающихся строить графики функций путем преобразования графика данной функции, применяя параллельный перенос, сжатие (растяжение), различные виды симметрии.

Воспитательная:

• Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность, умение работать в группе.
• Воспитывать интерес к предмету и потребности в приобретении знаний.

Развивающая:

• Развивать пространственное воображение и логическое мышление обучающихся, умение быстро ориентироваться в обстановке; развивать сообразительность, находчивость, тренировать память.

Оборудование:

• Мультимедийная установка: компьютер, проектор.

Литература:

1. Башмаков, М. И. Математика [Текст]: учебник для учреждений нач. и сред. проф. образования/ М. И. Башмаков.- 5-е изд., испр. – М.: Издательский центр “Академия”, 2012. – 256 с.
2. Башмаков, М. И. Математика. Задачник [Текст]: учеб. пособие для образоват. учреждений нач. и сред. проф. образования/ М. И. Башмаков.– М.: Издательский центр “Академия”, 2012. – 416 с.

План урока:

1. Организационный момент (3 мин).
2. Актуализация знаний (7 мин).
3. Объяснение нового материала (20 мин).
4. Закрепление нового материала (10 мин).
5. Итог урока (3 мин).
6. Домашнее задание (2 мин).

Ход урока

1. Орг. момент (3 мин).

Проверка присутствующих.

Сообщение цели урока.

Основные свойства функций как зависимостей между переменными величинами не должны существенно меняться при изменении способа измерения этих величин, т. е. при изменении масштаба измерения и начала отсчета. Однако за счет более рационального выбора способа измерения переменных величин обычно удается упростить запись зависимости между ними, привести эту запись к некоторому стандартному виду. На геометрическом языке изменение способа измерения величин означает некоторые простые преобразования графиков, к изучению которых мы сегодня и перейдем.

2. Актуализация знаний (7 мин).

Прежде чем будем говорить о преобразованиях графиков, повторим пройденный материал.

Устная работа. (Слайд 2).

Даны функции:

3. Охарактеризуйте графики функций: , , , .

3. Объяснение нового материала (20 мин).

Простейшие преобразования графиков – это их параллельный перенос, сжатие (растяжение) и некоторые виды симметрии. Некоторые преобразования представлены в таблице (Приложение 1) , (Слайд 3).

Работа в группах.

Каждая группа строит графики заданных функций и представляет результат для обсуждения.

Функция	Преобразование графика функции	Примеры функций	Слайд
	Оу на А единиц вверх, если A >0, и на |A| единиц вниз, если А <0.	,	(Слайд 4)
	Параллельный перенос его вдоль оси Ох на а единиц вправо, если а >0, и на -а единиц влево, если а <0.	,	(Слайд 5)
,